Answer: 0.1255
Given the confidence interval proportion:
![0.567<p>We are going to solve for the margin of error. To do that, we must first solve for the sample proportion of the given confidence interval. We just need to get the average of the lower and upper bound confidence interval</p>[tex]\hat{p}=\frac{0.567+0.818_{}}{2}=0.6925]()
Now that we got the sample proportion, we can now solve for the margin of error based on the formula below:
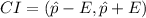
Now, since CI = ( 0.567, 0.818 ), we can solve this as:
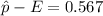
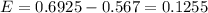
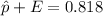
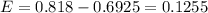
Therefore, the margin of error is 0.1255