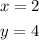Question

Solve the following system of equationy=3x-2y=-2x+8

Answer 1

From the present problem, it was given the following system of equations:

`\begin{gathered} \lbrack1\text{\rbrack} \\ y_1=3x_1-2 \\ \lbrack2\text{\rbrack} \\ y_2=-2x_2+8 \end{gathered}`

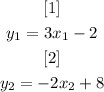
The solution for the given system is the coordinate pair (x, y) such as:

`\begin{gathered} x=x_1=x_2 \\ y=y_1=y_2 \end{gathered}`

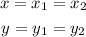
If we use the fact that y1 = y2, we are able to write the following:

`\begin{gathered} 3x_1-2=-2x_2+8 \\ \text{ but;. . . }x_1=x_2=x \\ 3x-2=-2x+8\to3x+2x=8+2\to \\ 5x=10\to x=(10)/(5) \\ x=2 \end{gathered}`

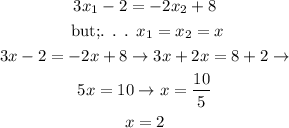
From this, we just need to substitute the value we calculated to x in any of the given equations. We will substitute it into the first one, to find the y value.

`\begin{gathered} y=3*2-2=6-2=4 \\ y=4 \end{gathered}`

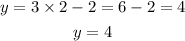
From the solution presented above, we are able to conclude that the solution for the given system of equations is:

`\begin{gathered} x=2 \\ y=4 \end{gathered}`