Question

Particles q1 = -53.0 uc, q2 = +105 uc, andq3 = -88.0 uc are in a line. Particles qi and q2 areseparated by 0.50 m and particles q2 and q3 areseparated by 0.95 m. What is the net force onparticle q3?Remember: Negative forces (-F) will point LeftPositive forces (+F) will point Right-53.0 C+105 με-88.0 με91+92930.50 m0.95 m

Answer 1

We have the next diagram

r12=0.5

r23=0.95

r13=1.45

Using Columb's law the net force of the particle q3 will be equal to the sum of the forces on particle q3 from particle q1 and q2.

the force between q1 and q3

`\begin{gathered} F_(13)=k\text{ }(q_1\cdot q_3)/(r^2_(13)) \\ F_(13)=9*10^9\text{ }((-53*10^(-6)\cdot-88*10^(-6)))/(1.45^2) \\ F_(13)=19.96N \end{gathered}`

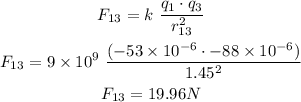
then for between q2 and q3

`\begin{gathered} F_(23)=k\text{ }(q_2\cdot q_3)/(r^2_(23)) \\ F_(23)=9*10^9\text{ }((105*10^(-6))\cdot(-88*10^(-6)))/(0.95^2) \\ F_(23)=-92.14N \end{gathered}`

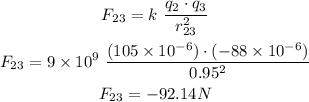
Then we analyze

`F_3=F_(13)+F_(23)=19.96-92.14=-72.18`

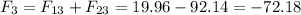
The force is 72.18N to the left