Question

Find the solution of the rational equation and identify any extraneous values (x + 7)/(x+10) = 4

Answer 1

x = -11

There aren't extran

Step-by-step explanation:

The initial equation is:

`(x+7)/(x+10)=4`

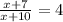
To solve the equation, we will multiply both sides by (x+10):

`\begin{gathered} (x+10)\cdot(x+7)/(x+10)=4\cdot(x+10) \\ x+7=4(x+10) \end{gathered}`

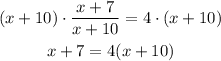
Then, we can apply distributive property on the right side, so:

`\begin{gathered} x+7=4x+4(10) \\ x+7=4x+40 \end{gathered}`

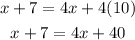
Now, we can solve the equation as:

`\begin{gathered} x+7-x=4x+40-x \\ 7=3x+40 \\ 7-40=3x+40-40 \\ -33=3x \\ -(33)/(3)=(3x)/(3) \\ -11=x \end{gathered}`

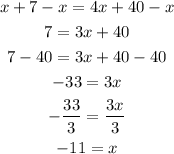
Therefore, the solution of the rational equation is x = -11

On the other hand, to identify the extraneous values, we need to replace the solutions on the initial equation, so replacing x = -11, we get:

`\begin{gathered} (-11+7)/(-11+10)=4 \\ (-4)/(-1)=4 \\ 4=4 \end{gathered}`

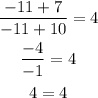
Since there isn't a problem when we replace x by -11, this solution is not an extraneous value.

So, the answer is x = -11 and there aren't extraneous values.