We have here a case of a linear function. In this case, we have that the linear function is given by:
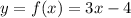
To fill the table, we need to substitute each value for the varible x into the function, asimplify the expression, and we will get the corresponding value for y (or f(x)). Therefore, we have:
For x = -3
Then we have:
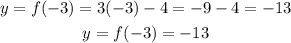
Therefore, for x = -3, we have that y (or f(x)) = -13
For x = -1
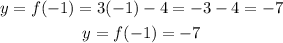
Then, for x = -1, y = -7
For x = 1
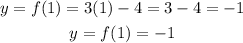
Then, for x = 1, y = -1.
For x = 3
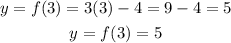
Then, for x = 3, y = 5
For x = 5
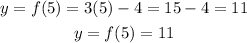
Then, for x = 5, y = 11.
In summary, therefore, we can comptete the table as follows:
x y or f(x)
-3 -13
-1 -7
1 -1
3 5
5 11