Given that:
A bee flies 10 ft/s directly towards a flowerbed from its hive.
It stays at the flowerbed for 15 minutes and then flies directly back to the hive at 8 ft/s.
The total time it is away from there is 19 minutes.
Consider that speed is the ratio of distance traveled to the time taken. That is:
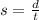
Let x represent the distance from the bee hive to the flowerbed, and d be the distance.
When speed was 10 ft/s, let the time be y

When the speed was 8 ft/s, let time be z
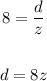
Distance is unchanged, so

Since the total time is 19 minutes = 1140 seconds
We have the equation for time as:

Solving (1) and (2) simultaneously, we can obtain the values for x and y, and these will help know the value for the required distance.