Question

The standard form of a quadratic equation is given as y=ax^2+bx+c and vertex form is given as y=a(x−h)^2+k. Write a formula that relates the values of a,b, and c in y=ax^2+bx+c to the values of a,h, and k in y=a(x−h)^2+k. For instance, h=ax+b would be a formula that relates h to a and b.

Answer 1

The minimum is at (1,-8). In the equation y = (x – 1)2 – 8, h = 1 and c = 8. So, the x-coordinate of the minimum is the same as the h-value in the equation, and the y-value of the minimum is the opposite of the c-value.

Step-by-step explanation:

plato

Answer 2

Answers:

`h = -(b)/(2a)\\\\k = (-b^2+4ac)/(4a)\\\\`

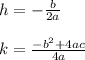
where 'a' cannot be zero.

=========================================================

Step-by-step explanation:

The vertex is (h,k)

The x coordinate of the vertex is h which is found through this formula

`x = -(b)/(2a)`

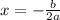
For example, if we had the quadratic
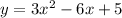`y = 3x^2-6x+5`, then we'll plug in a = 3 and b = -6 to get:
`h = -(b)/(2a) = -(-6)/(2*3) = 1`

------------

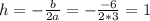
To find the value of k, we plug that h value into the original standard form of the quadratic and simplify.

`y = ax^2+bx+c\\\\k = ah^2+bh+c\\\\k = a\left((-b)/(2a)\right)^2+b\left((-b)/(2a)\right)+c\\\\k = a*(b^2)/(4a^2)+(-b^2)/(2a)+c\\\\k = (b^2)/(4a)+(-b^2)/(2a)+c\\\\`

`k = (b^2)/(4a)+(-b^2)/(2a)*(2)/(2)+c*(4a)/(4a)\\\\k = (b^2)/(4a)+(-2b^2)/(4a)+(4ac)/(4a)\\\\k = (b^2-2b^2+4ac)/(4a)\\\\k = (-b^2+4ac)/(4a)\\\\`

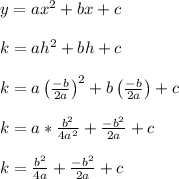
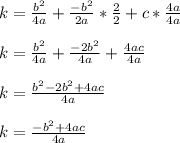
It's interesting how we end up with the numerator of
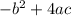`-b^2+4ac` which is similar to
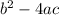`b^2-4ac` found under the square root in the quadratic formula. There are other ways to express that formula above. We need
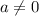`a \\e 0` to avoid dividing by zero. The values of b and c are allowed to be zero.