Question

Triangle MNO is transformed into triangle M'N'O'. What transformations were used. Reflection over the y-aixsReflection over the x-axisRotation 180o around the originDilation scale factor 2 with center at NDilation scale factor 1/2 with center at NRotation 90o clockwise around the origin

Answer 1

Reflection over the y axis

Dilation of 1/2 with center N

Step-by-step explanation:

To solve the question, we need to state the coordinates of both traingles and compare to get the transformations.

For triangle MNO:

M (-2, 4), N(0, 0) and O (-6, -2)

For triangle M'N'O':

M' (1, 2), N' (0, 0) and O' (3, -1)

from M to M', N to N' and O to O':

`\begin{gathered} (1)/(2)(-2,\text{ 4) = (-1, 2)} \\ (1)/(2)(0,\text{ 0) = (0, 0)} \\ (1)/(2)(-6,\text{ -2) = (-3, -1)} \end{gathered}`

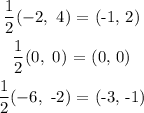
After a dilation of 1/2 was applied to the coordinates of the initial triangle, the coordinates above is almost equal to the coordinates of the new triangle except that the x coordinate was negated while keeping the y coordinate constant.

We need to find the transformation with this property: negating x while keeping y constant

A reflection of over the y axis is given as:

`\begin{gathered} (x,\text{ y) }\rightarrow\text{ (-x, y)} \\ \text{Here x is negated, y is constant} \\ \\ To\text{ confirm, }we\text{ will be negating the x coordinates }of\text{ the dilation we carried out} \\ \text{while k}eepi\text{ ng the y coordinates constant} \\ (-(-1),\text{ 2) = (1, 2) = M'} \\ (-(0),\text{ 0) = (0, 0) = N'} \\ (-(-3),\text{ -1) = (3, -1) = O'} \end{gathered}`

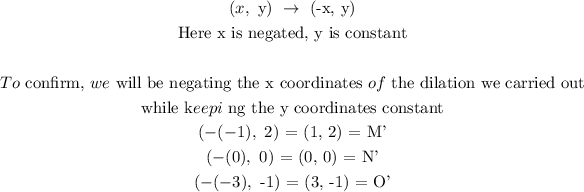
Hence, the transformations that transformed MNO into M'N'O' are:

Reflection over the y axis

Dilation of 1/2 with center N