To find the equation of the line that passes through 2 points, we have to find the slope and the y-intercept
The form of the equation is y = mx + b
m is the slope
b is the y-intercept
The rule of the slope is

Since the line passes through points (0, 7) and (3, 10), then
x1 = 0 and x2 = 3
y1 = 7 and y2 = 10
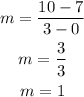
Substitute m in the rule of the equation
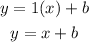
Since b is the y-intercept (value y at x = 0)
Since the line passes through the point (0, 7), then
b = 7
The equation of the line is

The answer is C