Step 1
Given;
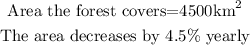
Required; To find area after 12 years
Step 2
State the formula for the population decrease
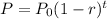
where;
![\begin{gathered} P_0=4500\operatorname{km} \\ r=(4.5)/(100)=0.045 \\ t=12 \\ P=\text{ Area after a given period of time in the case 12 years} \end{gathered}]()
Step 3
Find the area after 12 years
![\begin{gathered} P=4500(1-0.045)^(12) \\ P=4500(0.955)^(12) \\ P=2589.720966 \\ P\approx2589.72\operatorname{km}^2\text{ } \end{gathered}]()
Hence, the area the forest will cover after 12 years approximately to decimal places will be = $2589.72 km²