The equations of the line and the curve are
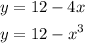
We will equate their right sides to find the values of x
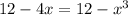
Subtract 12 from both sides

Divide both sides by -1
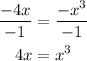
Subtract 4x from both sides
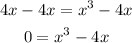
Switch the two sides
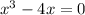
Take x as a common factor
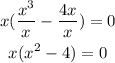
Factor the bracket using the rule of the difference between two squares
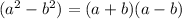
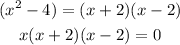
Now, equate each factor by 0

Substitute the values of x in the equation of the line to find their corresponding values of y
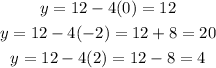
The points of intersection between the line and the curve are
(0, 12), (-2, 20), (2, 4)
Let us draw the graph
The red line represents the equation of the line
The blue curve represents the equation of the curve
To find the area bounded between the line and the curve we will use the integration
Since the line is above the curve at the point (-2, 20), then
We will subtract the curve from the line and use the values of x -2 and 2 as the limits of integration
![A=\int_(-2)^2[(12-4x)-(12-x^3)]dx](https://img.qammunity.org/2023/formulas/mathematics/college/owojozvjrh4vvotf43j659usmp361qfofu.png)
Simplify the terms inside the brackets first.
![\begin{gathered} A=\int_(-2)^2[12-4x+12+x^3]dx \\ A=\int_(-2)^2[-4x+x^3]dx \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/tme1b9agy2jcti8df7do0xmfqwacrahvdv.png)
In integration, we will add the power by 1 and divide the term by the new power
![A=[(-4x^(1+1))/(1+1)+(x^(3+1))/(3+1)]_(-2)^2](https://img.qammunity.org/2023/formulas/mathematics/college/wodd7txlqnh46jh27mo5g98y67k92f9mn3.png)
Simplify it
![\begin{gathered} A=[(-4x^2)/(2)+(x^4)/(4)]_(-2)^2 \\ A=[-2x^2+(x^4)/(4)]_(-2)^2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/d4zq48txfn9i9qejc4knsg8q6c2g11biz7.png)
Substitute x by 2 and -2, then subtract the answer
![A=[-2(2)^2+(2^4)/(4)]-[-2(-2)^2+((-2)^4)/(4)]](https://img.qammunity.org/2023/formulas/mathematics/college/gim16b4tfpq608u6k6xy28lj3dt78oa2lf.png)
Solve each bracket
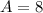
The area of the region bounded between the line and the curve is 8 square unit