Question

Which of the following functions arecontinuous on the interval 0 < 2 < 2?

Answer 1

Notice that:

`1^2-1=0.`

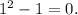
Therefore:

`f(x)=(x-1)/(x^2-1)`

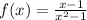
is undefined at x=1.

Now, recall that the natural logarithm is defined over the positive numbers, therefore:

`x^2-1>0`

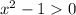
Then:

`x>1\text{ or }x<-1.`

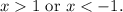
Therefore the function

`f(x)=ln(x^2-1)`

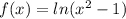
is not well defined over the interval (0,2).

Finally, notice that:

`p(x)=x^2+1,`

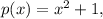
has no real zeros, therefore the function:

`f(x)=(x+1)/(x^2+1)`

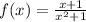
is well defined over all real numbers, also is continuous over all real numbers, particularly over the interval (0,2).

Answer: First option.

II only.