Given the equation:
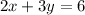
You need to substitute the coordinates of each ordered pair into the Linear Equation and then evaluate. If the left side of the equation and the right side are equal, then that ordered pair is a solution to the Linear Equation:
A. For:
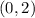
You can identify that:
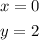
Then, substituting values and evaluating, you get:
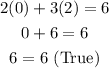
Therefore, it is a solution to the equation.
B. For:
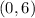
You get:
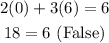
Therefore, it is not a solution to the equation.
C. For:
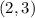
You get:
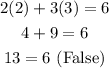
Notice that it is not a solution to the equation.
D. For:
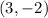
You get:
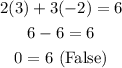
It is not a solution to the equation.
E. For:
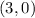
You get:
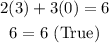
Therefore, it is a solution to the equation.
F. For:
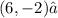
You obtain that:
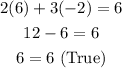
Therefore, it is a solution to the equation.
Hence, the answer is:
- Option A.
- Option E.
- Option F.