Question

Write the limit as a definite integral on the interval [a, b], where ci is any point in the ith subinterval.

Answer 1

Step-by-step explanation

We have the following integral in the discrete sum form:

`\lim_(||\Delta||\to0)\sum_{i\mathop{=}1}^(\infty)(6c_i+3)\Delta x_i.`

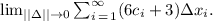
In the interval [-9, 6].

To convert to the integral form, we convert each element of the discrete sum form:

`\begin{gathered} \lim_(||\Delta||\to0)\sum_{i\mathop{=}1}^(\infty)\rightarrow\int_(-9)^6 \\ 6c_i+3\rightarrow6x+3 \\ \Delta x_i\rightarrow dx \end{gathered}`

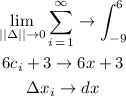
Replacing these in the formula above, we get the integral form:

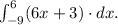
`\int_(-9)^6(6x+3)\cdot dx.`Answer