This is the solution to a 2 degree equation:
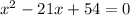
The two numbers that multiply to 54 and add to -21 are the roots of this equation.
We can find the solution of an equation with this form:

With this formula:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
For this problem, a = 1, b = -21 and c = 54:
![x=\frac{21\pm\sqrt[]{(-21)^2-4\cdot1\cdot54}}{2\cdot1}=\frac{21\pm\sqrt[]{441-216}}{2}=\frac{21\pm\sqrt[]{225}}{2}=(21\pm15)/(2)](https://img.qammunity.org/2023/formulas/mathematics/college/7rcx69usp7ng7tkbclzna1npdlhfa1bzsg.png)
The two numbers are:
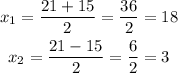
The numbers are -18 and -3 (they must be negative so they add up to a negative number)