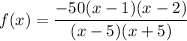Answer:
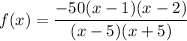
Explanation:
Since f(x) has asymptotes at x = 5 and x = -5, then the denominator of the rational function contains the terms (x - 5) and (x + 5):
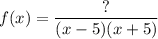
Since f(x) has x-intercepts at x = 2 and x = 1, then the numerator of the rational function contains the terms (x - 2) and (x - 1):
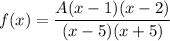
Now substitute the point (0, 4) and solve for A:
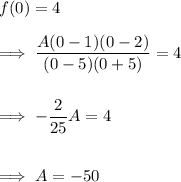
So final rational function: