Question

An ice cream store has the pricing shown below. You want to determine the best value. The height of the cone is 4.5 in and the diameter is 2 in. The diameter of each scoop is 3 in. Assume the cone is stuffed full with ice cream.Question: Which size is the best value? Explain your reasoning using complete sentences.

Answer 1

Step 1:

We will calculate the volume of ice cream in the single scoop

The volume of the ice cream will be

`\begin{gathered} V=(1)/(3)\pi r^2h+(2)/(3)\pi r^3 \\ r=(2in)/(2)=1in(cone) \\ h=4.5in \\ r=(3in)/(2)=1.5in(radius\text{ of the hemisphere\rparen} \end{gathered}`

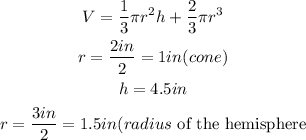
By substituting the values, we will have

`\begin{gathered} V=(1)/(3)\pi r^(2)h+(2)/(3)\pi r^(3) \\ V=(1)/(3)*(22)/(7)*1^2*4.5+(2)/(3)*(22)/(7)*1.5^3 \\ V=(33)/(7)+(99)/(14) \\ V=(165)/(14) \\ V=11.79in^3 \end{gathered}`

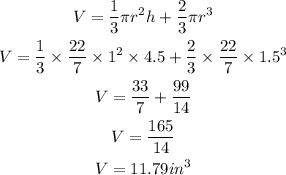
Step 2:

We will use the formula below to calculate the volume of the two scoops of ic cream

`\begin{gathered} V=(1)/(3)\pi r^2h+(4)/(3)\pi r^3 \\ V=(1)/(3)*(22)/(7)*1^2*4.5in+(4)/(3)*(22)/(7)*1.5^3 \\ V=(33)/(7)+(99)/(7) \\ V=(132)/(7) \\ V=18.86in^3 \end{gathered}`

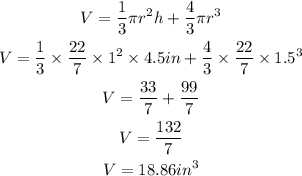
Step 3:

We will use the formula below to calculate the volume of the three scoops of ic cream

`\begin{gathered} V=(1)/(3)\pi r^2h+(6)/(3)\pi r^3 \\ V=(1)/(3)*(22)/(7)*1^2*4.5+2*(22)/(7)*1.5^3 \\ V=(33)/(7)+(297)/(14) \\ V=(363)/(14) \\ V=25.93in^3 \end{gathered}`

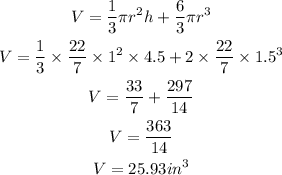
For the first ice cream with one scoop

`\begin{gathered} 1in^3=(3.50)/(11.79) \\ 1in^3=\text{ \$}0.30 \end{gathered}`

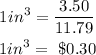
For the second ice cream with two scoops

`\begin{gathered} 1in^3=(4.50)/(18.86) \\ 1in^3=\text{ \$}0.24 \end{gathered}`

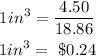
For the third ice cream with three scoops

`\begin{gathered} 1in^3=(5.50)/(25.93) \\ 1in^3=\text{ \$}0.21 \end{gathered}`

Hence,

The final answer is

The triple sold at $5.50 has the best value because it has the lowest price of $0.21 per cubic inch of the ice cream