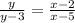1 Answer

Emery · Answer 1 · 2023-06-06T10:56:18+0000

SOLUTION

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the given points on the graph

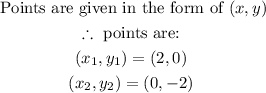
$\begin{gathered} \text{ Points are given in the form of }(x,y) \\ \therefore\text{ points are:} \\ (x_1,y_1)=(2,0) \\ (x_2,y_2)=(0,-2) \end{gathered}$

STEP 2: Write the slope-intercept form of the equation of a line

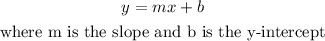
$\begin{gathered} y=mx+b \\ \text{where m is the slope and b is the y-intercept} \end{gathered}$

STEP 3: Write the formula to get the equation of a line using two given points

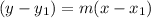
STEP 4: We use the given points to get the slope

STEP 5: Substitute the given points into the formula in step 4 to get the slope

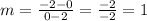
STEP 6: Since we have a slope and two points, we use the formula in step 3 to get the function that represents the line

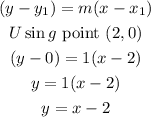
$\begin{gathered} (y-y_1)=m(x-x_1) \\ U\sin g\text{ point }(2,0) \\ (y-0)=1(x-2) \\ y=1(x-2) \\ y=x-2 \end{gathered}$

STEP 7: We get the rational function of the line using the given hole

$\begin{gathered} \text{hole}=(5,3) \\ \text{equation of line }\Rightarrow y=x-2 \\ \\ To\text{ get the rational function, we write the function of each coordinate that makes it undefined} \\ (5,3)\Rightarrow x=5\Rightarrow x-5 \\ (5,3)\Rightarrow y=3\Rightarrow y-3 \\ We\text{ divide the equation of the line in step 6 by the expressions above} \\ \text{Hence, the rational function is given as:} \\ (y)/(y-3)=(x-2)/(x-5) \end{gathered}$

Hence, the rational function representing the line with the given hole is:

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions