In order to sculpt the lion, the scupltor must have, at least, a rectangular composite that has the maximum dimensions of the final sculpture.
Thereby,
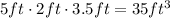
The rectangular composite would need to have a volume of 35 cubic feet.
Now, let's use a rule of three to calculate the weight of the composite, since we're given its density:
This way,
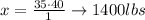
We can conclude that the weight of the smallest rectangular block that the sculptor must purchase in order to create his statue is 1400 lbs