To solve the absolute value equation;
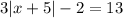
Note that the left side of the equation is an absolute value. The first step is to remove the absolute value sign, and then the next step is to solve while using the positive and negative value of the number on the right side of the equation.
This is shown below;
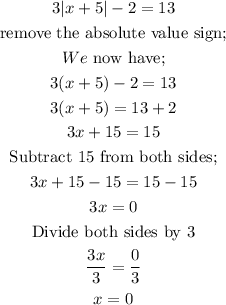
Let us now solve for the equation when the right side is -13.

ANSWER:
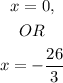
The last option is the correct answer