a)
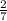
b)
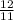 Step-by-step explanation
Step-by-step explanationThe probability of an event occurring is intuitively understood to be the likelihood or chance of it occurring, the probability is givenby:
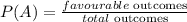
so
Step 1
we can find the odds in favor by using the expression:
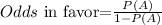
so
let
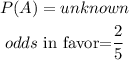
now, replace and solve for P(A)

therefore, the probabilyt of winning a new TV is
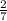
Step 2
now, to find the odds against we need to use the formula:
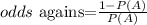
so
let
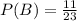
now, replace in the formula and calculate

therefore, the odds against are
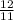
I hope this helps you