SOLUTION
The odd numbers in a six sided die are 1, 3 and 5. That is 3 numbers
The numbers less than four are 1, 2 and 3. That is 3 numbers
The probability of rolling an odd number becomes

Probability of rolling a number less than 4 becomes
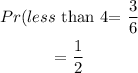
Now looking at the odd numbers and the numbers less 4, we have
1, 3, 5 and 1, 2, 3. So between these numbers are 1 and 3. which is 2. Probability of this is
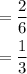
Hence the probability of rolling an odd number or a number less than 4 becomes

Hence the answer is 2/3