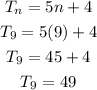Answer:
The common difference, d = 5
Step-by-step explanation:
The given sequence is:
9, 14, 19
The common difference is the difference between the consecutive terms of the sequence.
The common difference, d = 14 - 9 or d = 19 - 14
Therefore, the common difference, d = 5
The nth term of an Arithmetic sequence is given by the formula:
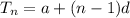
where the first term, a = 9
The common difference, d = 5
Substitute a = 9, and d = 5 into the nth term formula above
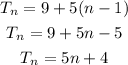
The 9th term in the sequence is calculated by substituting n = 9 into the nth term gotten above