Question

The jones brother, Carl,Cameron, and Carlos, are painters. Together they can paint a standard sized room in 2 hours. If Carl is alone on the job he can paint the room in 5 hours. If Cameron is alone he can paint the room in 6 hours.a)what equation can be used to determine how long it would take Carlos to paint the room alone? b)How long would it take Carlos to paint the room alone?

Answer 1

The workdone by the three(3) is equal to the painting of 1 room in 2 hours.

Time taken by

Carl alone = 5 hours

Cameron alone = 6 hours

Let time taken by Carlos alone = x hours

In One(1) hour, the size of the that will be covered by each of them is:

`\begin{gathered} \text{Carl alone = }(1)/(5)\text{ of the room} \\ \text{Cameron alone=}(1)/(6)\text{ of the room} \\ \text{Carlos alone= }(1)/(x)\text{ of the room} \end{gathered}`

a) Hence, the equation that can be used to determine how long it would take Carlos to paint the room alone is:

`(1)/(5)\text{ + }(1)/(6)\text{ + }(1)/(x)=(1)/(2)`

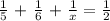
b) We will solve for the value of x in the equation above

`\begin{gathered} (1)/(5)\text{ + }(1)/(6)\text{ + }(1)/(x)=\text{ }(1)/(2) \\ \\ (1)/(x)=(1)/(2)\text{ - }(1)/(5)\text{ - }(1)/(6) \\ \\ (1)/(x)=(15-6-5)/(30) \\ \\ (1)/(x)=(4)/(30) \\ \\ x=(30)/(4) \\ x=(15)/(2) \\ x=7.5\text{ hours} \end{gathered}`

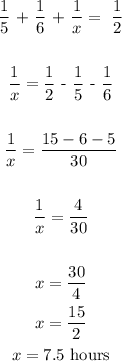
Hence, it will take Carlos 7.5 hours to paint the room alone