Question

. dv/dt = a and dx/dt = v(t) where a is constant.Find v(t) in terms of v(0), and a.a.b. Find x(t) in terms of x(0), v(0) and a.

Answer 1

Given:

`\begin{gathered} (dv)/(dt)=a \\ (dx)/(dt)=v \end{gathered}`

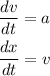
a is a constant

To find:

(a) v(t) in terms of v(0), and a

(b) x(t) in terms of x(0), v(0) and a

Step-by-step explanation:

(a) We can write,

`dv=adt`

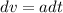
Integrating both sides we can write,

`\begin{gathered} \int_(v(0))^(v(t))dv=\int_0^tadt \\ v(t)-v(0)=at \\ v(t)=v(0)+at \end{gathered}`

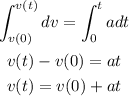
Hence, the velocity is,

`v(t)=v(0)+at`

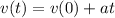
(b)

We can also write,

`\begin{gathered} (dx)/(dt)=v(t) \\ dx=v(t)dt \end{gathered}`

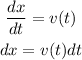
Integrating both sides we get,

`\begin{gathered} \int_(x(0))^(x(t))dx=\int_0^tv(t)dt \\ \int_(x(0))^(x(t))dx=\int_0^t[v(0)+at]dt \\ x(t)-x(0)=v(0)t+(1)/(2)at^2 \\ x(t)=x(0)+v(0)t+(1)/(2)at^2 \end{gathered}`

Hence,

`x(t)=x(0)+v(0)t+(1)/(2)at^2`