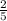Let Δx be an increase in the variable such that 0.9x increases by 2π. Then:
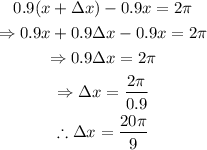
The period of a function f is a quantity T such that for every x, then:
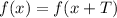
The cosine function has a period of 2π over its argument. In this case, we know that:
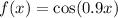
The argument of cosine is 0.9x and we already know that for an increase of 20π/9 in x, there is an increase of 2π in 0.9x. Therefore:
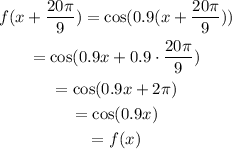
Then, for every x we know that:
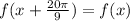
Therefore, the period of f is:
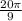
Following a similar process, we can find the period of the function g. Since we know that the period of the sine function is also 2π.
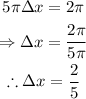
Therefore, the period of g is: