Question

George wants his airplane to travel along a path that is [60°] with a groundspeed of 280 km/h. If the wind is blowing from the direction [10°] at 65 km/h, then in what direction should the pilot steer towards and what would be his airspeed? use the component method please

Answer 1

We know that the groundspeed we want is of 280 km/h with a direction of 60° and that the wind is blowing with a speed of 65 km/h with a direction of 10°; this vectors are shown in the diagram below:

Let v be the vector of the speed of the plane. We know that the 280 km/h vector will be the sum of the aispeed vector and the wind vector, that is:

`\begin{gathered} \vec{r}=\vec{v}+\vec{w} \\ \text{ where} \\ \vec{r}\text{ is the 280 km/h vector } \\ \vec{w}\text{ is the wind vector} \end{gathered}`

We know that the any given vector can be decomposed as:

`\vec{v}=\langle v\cos\theta,v\sin\theta\rangle`

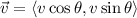
For the resultant vector we have a magnitude of 280 km/s and a direction of 150° (with respect to the x-axis) and for the wind vector the magnitude is 65 km/h and the direction is 10°, then we have:

`\begin{gathered} \langle280\cos150,280\sin150\rangle=\vec{v}+\langle65\cos10,65\sin10\rangle \\ \vec{v}=\langle280\cos150,280\sin150\rangle-\langle65\cos10,65\sin10\rangle \\ \vec{v}=\langle-306.5,128.7\rangle \end{gathered}`

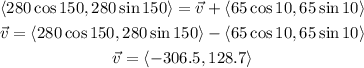
Now that we have vector v is component form we can calculate its magnitude and direction; remember that they are given by:

`\begin{gathered} v=√(v_x^2+v_y^2) \\ \theta=\tan^(-1)\lvert{(v_y)/(v_x)}\rvert \end{gathered}`

Then we have:

`\begin{gathered} v=√((-306.5)^2+(128.7)^2)=332.4 \\ \theta=\tan^(-1)\lvert{(-306.5)/(128.7)}\rvert=67.2 \end{gathered}`

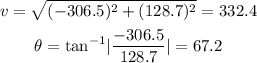
Now, we need to be careful with the angle, in this case vector v will lie in the second quadrant; which means that the angle is measure from west to north.

Therefore, the airspeed is 332.4 km/h and the direction will be W67.2°N