Given:
given functions are
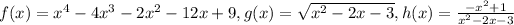
Find:
(A) we have to compare the Domain and range of the function f(x) and g(x).
(B) We have to find the relationship between the break of h(x) and zeros of f(x).
Step-by-step explanation:
The domain and Range of f(x) is
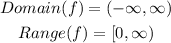
Domain and Range of g(x) is
![\begin{gathered} Domain(g)=(-\infty,-1]\cup[3,\infty) \\ Range(g)=[0,\infty) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/mvowv86v0p0ctsbweitdeilskk0t1i5aut.png)
Domain of h(x) is

Now zeros of the function f(x) are
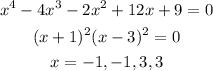
Therefore, zeors of the function f(x) are -1,-1,3,3.
Now,
(A)The difference between Domain of f(x) and g(x) is of the interval (-1,3). The domain of f(x) is all Real Numbers and Domain of g(x) is all the real number except the interval (-1,3).
The Range of both f(x) and g(x) is same.
(B) The breaks in the Domain of h(x) are equal to the zeros -1, 3 of f(x).