To draw the histogram, first, you have to order the given data set in class intervals.
It is given that you have to determine 5 class intervals of equal width, that the initial class boundary must be 13.5 and the ending class boundary must be 48.5.
To determine the width you have to use for the class intervals, you have to calculate the difference between the ending class boundary and the initial class boundary, and divide the result by the number of class intervals:
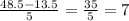
The width of each interval must be 7 units.
Next, you have to determine the intervals, for this, you have to add the calculated width to the initial class boundary:
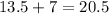
The bounds of the first class interval are: [13.5; 20.5)
Next, add the width to the right bound of the previous interval to determine the next one:
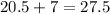
The second interval is [20.5; 27.5)
Repeat the process to determine the next three intervals:
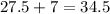
The third interval is [27.5; 34.5)
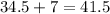
The fourth interval is [34.5;41.5)
And finally, the fifth interval is [41.5;48.5]
Once you have determined the intervals you have to construct a frequency table using the given data set:
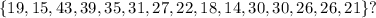
-First, order the values from least to greatest:
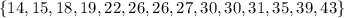
Next, count how many numbers correspond to each class interval and construct the table.
For example for the first interval [13.5;20.5) correspond all values are greater than or equal to 13.5 and less than 20.5. Those values are "14, 15, 18, 19", the frequency for this interval is 4.
The frequency table is:
The next step is to construct the histogram. In the x-axis you have to write down the intervals and in the y-axis you have to write the frequencies: