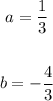Question

2. For the function below, find a and b such that f is differentiable everywhere.

Answer 1

Given the function:

`f(x)=\begin{cases}ax^3,x\leqslant{2} \\ x^2+b,x>2{}\end{cases}`

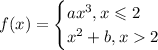
If the function is differentiable everywhere, this means that it should be differentiable for x = 2 too. Additionally, if it is differentiable in x = 2, it is continuous in x = 2.

For continuity, we have:

`\begin{gathered} a(2)^3=2^2+b \\ \\ \Rightarrow b=8a-4...(1) \end{gathered}`

For differentiability, we have:

`\begin{gathered} 3a(2)^2=2(2) \\ 12a=4 \\ \\ \Rightarrow a=(1)/(3)...(2) \end{gathered}`

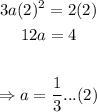
Using (2) in (1):

`\begin{gathered} b=(8)/(3)-4 \\ \\ \Rightarrow b=-(4)/(3) \end{gathered}`

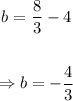
Summarizing:

`\begin{gathered} a=(1)/(3) \\ \\ b=-(4)/(3) \end{gathered}`