A generic graph would be
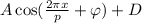
Where:
A = amplitude
p = period
φ = phase
D = middle line
First let's evaluate the period of the function, see that x = -1/4 we have y = 5, it will have again at x = 3/4.
The period is

Let's put it in our function already
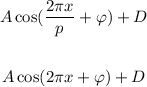
To find out the amplitude, we take the max value, the minimum value (all in modulus) and take the average, the max value here is 5 and the minimum -3 (in modulus it's 3), the average is
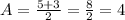
Therefore
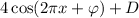
And the D value will be the average too, of the maximum two, but here we don't use the modulus on negative values, therefore
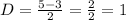
Hence.
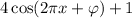
We know that when x = 0 we have y = 1, then
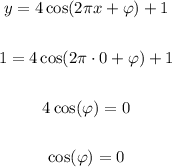
When cos(φ) = 0? when φ = π/2 for example. Of course, there are other solutions but we just need one. Now we have all the parameters of our cosine

The final answer is:
