1:5
Step-by-step explanation
Equivalent Fractions of 9/45 are fractions that are different than 9/45, but still have the same value, to maintain the ratio, we need to find a number that keeps the proportion
so
Let
Step 1
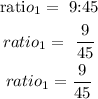
then, Let x represents the missing value, so
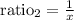
as the ratios are equivalent, we have a proportion

finally, solve for x
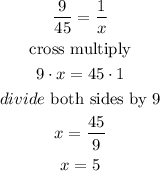
therefore, the answer is
1:5
I hope this helps you