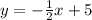we must find a line perpendicular to
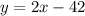
which passes through (-6,8). As we can see, this given lines has slope m=2.
First, the slope of a perpendicular line is the reciprocal inverse of the given line. In other words,
the perpendicular lines must have slope M equal to
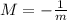
In our case m=2, hence, the perpendicular line has slope
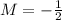
Therefore, the perpendicular line has the form
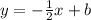
and now, we must find the y-intercept b. This can be done by substituying the given point (-6,8)
into the last equation:
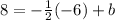
which gives
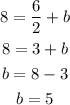
Finally, the answer is