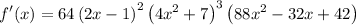To solve this question we going to need to formulas:
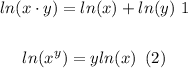
Now to make a logarithmic differentiation we apply logarithm to the initial equation
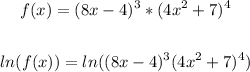
Now we apply the first two formulas
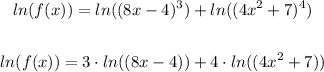
Now we make an implicit derivate
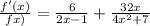
Simplify
![\frac{f^(\prime)(x)}{f\operatorname{\lparen}x)}=(88x^2-32x+42)/(\left(2x-1\right)\left(4x^2+7\right))]()
Now we are almost done but we have that f(x), but we know what is that from the beginning, f(x) = (8x - 4) ^ 3 * (4x ^ 2 + 7) ^ 4
Replacing
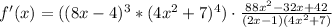
Answer:
Simplify