ANSWER:
3.47 m/s
Explanation:
We can calculate the velocity value assuming that the kinetic energy is equal to potential, therefore:
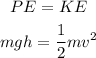
By losing 18% of initial energy, it means that the energy value is 82% (100-18), which means that the speed also represents 82%.
We replace the values and calculate for v, like this:
![\begin{gathered} 0.82\cdot mgh=(1)/(2)mv^2 \\ v=\sqrt[]{2gh} \\ v=\sqrt[]{0.82\cdot2\cdot9.8\cdot0.75} \\ v=3.47\text{ m/s} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/8qkn6895eli66c9mremuh4ivnn3tzy9taz.png)