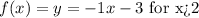You need to find the functions for each part of the graph.
All 3 parts are linear functions, given by the general form
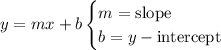
You can find the slope as follows:
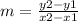
Let's evaluate a pair of points in each part of the graph to find the correspondent slope:
Part 1. Point 1 = (-2, 0) and Point 2= (0, 2)
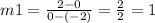
The y-intercept is the point where it crosses the y-axis, for the first part of the graph you can see it at y=2, then b=2
The function of this part is then:
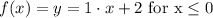
Part 2. Point 1 = (0, 1) and Point 2= (1, 1.4)
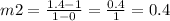
The y-intercept is at b=1, then the function for the second part is:
![f(x)=y=0.4x+1\text{ for 0<strong>Part 3. </strong>Point 1 = (3, -6) and Point 2= (4, -7)[tex]m3=(-7-(-6))/(4-3)=(-7+6)/(1)=-1]()
In this case, we can't see the point where the function crosses the y-axis, thus we need to evaluate the general form of the linear equation, replacing the slope and one of the known points

The function for the third part is: