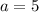Answer:
The value of a is;
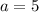
Step-by-step explanation:
Given a quadratic equation;
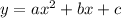
The values of x and y are given in the table.
to get the value of c,
at x =0, y=2.
let us substitute into the equation;
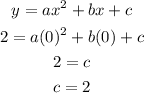
Since, we have the value of c. the equation becomes;
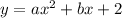
let us proceed to find a and b.
at x=-1, y=16
also at x=1,y=-2
let us substitute the two values;
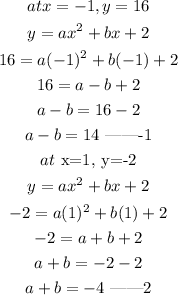
To get a add equation 1 and 2 together;
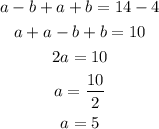
Therefore, the value of a is;