Question

How much flour did she need to make both cakes?

Answer 1

Given:

a.) April was making two different cakes.

b.) One cake recipe needed 7/9 cup of flour.

c.) The other cake needed 5/9 cup of flour.

Determining how many cups will April be needing means we will be adding the number of cups needed on each cake.

Since 7/9 and 5/9 are like fractions (with the same denominator), we can directly add the two fractions.

To do this, we just add the numerator and copy the denominator.

We get,

`\text{ }\frac{\text{ 7 }}{\text{ 9 }}\text{ + }\frac{\text{ 5 }}{\text{ 9 }}`
`\text{ = }\frac{\text{ 7 + 5}}{\text{ 9}}`
`\text{ = }\frac{\text{ 12 }}{\text{ 9 }}`
`\text{ = }\frac{\text{ 4 }}{\text{ 3 }}\text{ or 1 }(1)/(3)\text{ cups}`

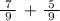
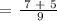
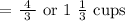
Therefore, April will be needing 4/3 or 1 1/3 cups of flour to make the two cakes.