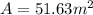Question

Find the area of this figure around your answer to the nearest hundredth

Answer 1

To answer this question, we have to find the are of the triangle, the rectangle, and the half of the circle (semicircle). Then we can proceed as follows:

Area of the triangle

It is given by the formula:

`\begin{gathered} A_{\text{triangle}}=(b\cdot h)/(2) \\ b=3m \\ h=5m \end{gathered}`

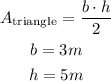
From the figure, we can see the values of the base, b = 3m, and the height of the triangle, h = 5m. Then we have:

`\begin{gathered} A_{\text{triangle}}=(b\cdot h)/(2) \\ A_{\text{triangle}}=(3m\cdot5m)/(2)=(15m^2)/(2) \\ A_{\text{triangle}}=7.5m^2 \end{gathered}`

Therefore, the area of the triangle is equal to 7.5 square meters.

Area of the rectangle

We know that the area of the rectangle is given by:

`\begin{gathered} A_{\text{rectangle}}=b\cdot h \\ b=6m \\ h=5m \\ A_{\text{rectangle}}=6m\cdot5m=30m^2 \\ A_{\text{rectangle}}=30m^2 \end{gathered}`

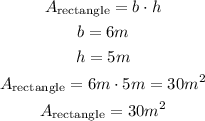
To find this area, we needed to multiply the base, b = 6m, times the height, h = 5m.

Therefore, the area of the rectangle is 30 square meters.

Area of the semicircle

We have that the area of a circle is given by:

`A_{\text{circle}}=\pi r^2`

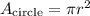
Where

• π = 3.14 (we will use this value for π)

,

• r is the radius of the circle

However, we need the area of the semicircle - half of the circle:

`A_{\text{semicircle}}=(1)/(2)\pi r^2`

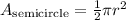
We also need the value for the radius. The radius is half the diameter of the circle. In this case, the diameter of the circle is d = 6m. Therefore:

`\begin{gathered} r=(d)/(2)\Rightarrow r=(6m)/(2)=3m \\ r=3m \end{gathered}`

Then, we have:

`\begin{gathered} A_{\text{semicircle}}=(1)/(2)\pi r^2 \\ A_{\text{semicircle}}=(1)/(2)\cdot3.14\cdot(3m)^2 \\ A_{\text{semicircle}}=(1)/(2)\cdot3.14\cdot9m^2 \\ A_{\text{semicircle}}=14.13m^2 \end{gathered}`

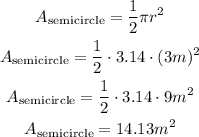
Therefore, the area of the semicircle is 14.13 square meters.

Now, the area of the figure is the sum of the areas of the triangle, rectangle, and semicircle:

`\begin{gathered} A_{\text{fig}}=A_{\text{triangle}}+A_{\text{rectangle}}+A_{\text{semicircle}} \\ A_{\text{fig}}=7.5m^2+30m^2+14.13m^2 \\ A_{\text{fig}}=51.63m^2 \end{gathered}`

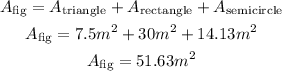
Therefore, in summary, the area of the figure is (to the nearest hundredth):

`A=51.63m^2`