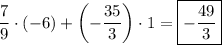Question

Evaluate the coefficient of x^5 and x^4 in the binomial expansion of (x/3-3)^7. Hence find the coefficient of x^5 in (x/3-3)^7(x-6)

Answer 1

Recall the binomial theorem:

`\displaystyle (a + b)^n = \sum_(k=0)^n \binom nk a^(n-k) b^k`

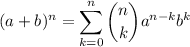
where
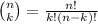`\binom nk = (n!)/(k!(n-k)!)` is the binomial coefficient.

Take a = x/3, b = -3, and n = 7. Then we get the x⁵ and x⁴ terms when 7 - k = 5 and 7 - k = 4, respectively; or when k = 2 and k = 3.

`k=2 \implies \dbinom 72 \left(\frac x3\right)^(7-2) (-3)^2 = 21 \cdot (x^5)/(243) \cdot 9 = \frac79 x^5`

`k=3 \implies \dbinom 73 \left(\frac x3\right)^(7-3) (-3)^3 = 35 \cdot (x^4)/(81) \cdot (-27) = -\frac{35}3 x^4`

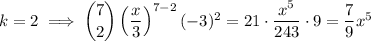
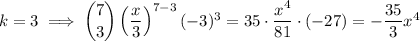
Then when multiplying this expansion by x - 6, we get an x⁵ terms from the products

`\frac79 x^5 \cdot (-6)`

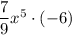
and

`-\frac{35}3 x^4 \cdot x`

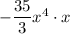
so that the x⁵ term in the overall expansion of (x/3 - 3)⁷ (x - 6) has a coefficient of

`\frac79\cdot(-6) + \left(-\frac{35}3\right) \cdot 1 = \boxed{-\frac{49}3}`