Question

1) Body temperatures of healthy adults is normally distributed with a mean of 98.20°F and astandard deviation of 0.62°F. Using Chebyshev's Theorem, what is the approximatepercentage of healthy adults with body temperatures between 97.58°F and 98.82°F? 2) GRE verbal reasoning scores has an unknown distribution with a mean of 150.1 and astandard deviation of 9.4. Using the empirical rule, what do we know about thepercentage of GRE verbal reasoning scores between 131.3 and 168.9?

Answer 1

Chebyshev's inequality cannot be used to determine the percentage of patients within 97.58°F and 98.82°F because it is only one standard deviation in width

SOLUTION

Problem Statement

The question tells us the temperature of healthy adults is normally distributed with a mean of 98.20℉ and a standard deviation of 0.62℉. We are asked to use Chebyshev's theorem to approximate the percentage of healthy adults with body temperatures between 97.58℉ and 98.82℉.

Method

To solve this question, we need to know the definition of Chebyshev's theorem and use it to answer the question.

Chebyshev's Theorem:

"Chebyshev’s Theorem estimates the minimum proportion of observations that fall within a specified number of standard deviations from the mean."

It is also known as Chebyshev's inequality and the inequality is written out as:

`\begin{gathered} \text{ At least (}1-(1)/(k^2))\text{\% of data lie within }k\text{ standard deviations of the mean} \\ \text{That is,} \\ P\ge(1-(1)/(k^2))\text{ \%} \\ \text{where,} \\ P=\text{percentage} \end{gathered}`

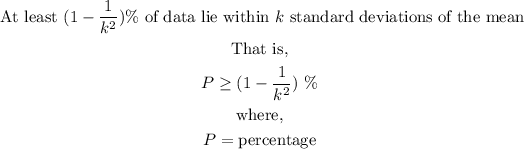
This means that if we can calculate the number of standard deviations (k) from the mean, we can approximate what percentage of the data must lie within that standard deviation range.

(Note: k cannot be 1 because Chebyshev's inequality would result in a zero on the right-hand side, implying that at least 0% of the data is within that standard deviation, which is useless for our purposes. This is why Chebyshev's inequality is not defined for a single standard deviation from the mean)

Thus, with this information, we can proceed to solve the question in the following steps:

Step 1: Calculate the number of Standard Deviations the values are from the mean.

We can make this calculation using the following:

`\begin{gathered} \text{Let the first value be }V_1 \\ \text{Let the second value be }V_2 \\ \mu-V_1=n\sigma \\ V_2-\mu=m\sigma \\ \text{where,} \\ m\text{ and n are the numbers of values over and below the mean respectively.} \\ (m+n)/(2)=k\text{ standard deviations from the mean} \end{gathered}`

Step 2. Use Chebyshev's inequality to approximate the percentage of healthy adults with body temperatures between 97.58 and 98.82 degrees Fahrenheit.

Implementation

Step 1: Calculate standard deviations:

`\begin{gathered} V_1=97.58^0F \\ V_2=98.82^0F \\ \mu=98.20^0F \\ \sigma=0.62^0F \\ \\ \therefore\mu-V_1=n\sigma \\ 98.20-97.28=n(0.62) \\ \therefore n=(98.20-97.28)/(0.62)=1 \\ n=1 \\ \\ V_2-\mu=m\sigma \\ 98.82-98.20-m(0.62) \\ m=(98.82-98.20)/(0.62)=1 \\ m=1 \\ \\ \therefore k=(1+1)/(2)=1\text{ standard deviation away from the mean} \end{gathered}`

Step 2: Use Chebyshev's inequality:

Since we know that Chebyshev's inequality is not valid for 1 standard deviation, we can conclude that Chebyshev's inequality cannot be used to determine the percentage of patients within 97.58°F and 98.82°F

Final Answer

Chebyshev's inequality cannot be used to determine the percentage of patients within 97.58°F and 98.82°F because it is only one standard deviation in width