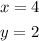Question

The graphs of several equation are shown at the right.State the solution of each system of equations.

Answer 1

By definition, a System of linear equations can have:

1. No solution: the lines are parallel, therefore they never intersect each other.

2. One solution: the lines intersect each other.

3. Infinitely many solutions: the graphs are the same line.

For this case, we can identify that the lines "a" and "b" intersect each other. That means that the System of equations has one solution. You can identify that the point of intersection is the following:

`(4,2)`

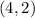
Where:

`\begin{gathered} x=4 \\ y=2 \end{gathered}`

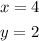
Therefore, the System of equations of the lines "a" and "b" has one solution:

`\begin{gathered} x=4 \\ y=2 \end{gathered}`