The nth term of an arithmetic sequence is given by the formula,
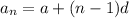
Here, 'a' denotes the first term, and 'd' denotes the common difference of the arithmetic sequence.
According to the given information,
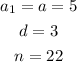
Substitute the values in the formula to obtain the 22nd term,
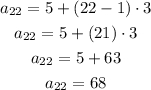
Thus, the 22nd term of the arithmetic sequ