In order to determine the area painted by Tico after 7 days of the increase rate, consider that the relation between area and days after the increase rate can be model by a linear equation (as you can notice in the given graph).
Let A the area and d the days, then, you can write, in a general way:
A - Ao = m(d - do)
where m is the slope of the line and (do,Ao) is any point on the line.
To find the value of m, use:
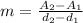
where (d1,A1) and (d2,A2) are any two points on the line. For instance, use:
(d1,A1) = (3,175)
(d2,A2) = (8,400)
Replace the previous values into the expression for m and simplify:
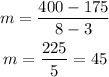
Now, use (do,Ao) = (3,175) and m=45 into the general equation of a line and solve for A:
A - 175 = 45(d - 3)
A - 175 = 45d - 135
A = 45d - 135 + 175
A = 45d + 40
Now, replace d = 7 into the previous equation:
A = 45(7) + 40
A = 315 + 40
A = 355
Hence. after 7 days of the increase in rate, the area painted by Tico is 355 cm^2