The regression line equation is given as
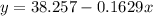
a.
When the truck has driven 100.000 miles, it means x = 100.000
Substitute x = 100.000 into the regression line equation
y = 38.257 - 0.1629(100.000)
y=38.257 - 16290
y= $21967
The price of the truck after driving 100.000 miles is $21967
b.Interprete the slope:
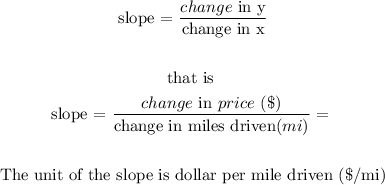
This can be interpreted as the the price for driving just 1 mile
Hence, the slope is the price that will cost to drive 1 mile
C. The y-intercept of the line
The y-intercept is where the line x = 0
This means the price of the Ford when mile covered is zero.
The is interpreted as the initial price of the Ford before it begins to cover any mile.