The given information is:
- The first row has 24 seats.
- Each row has 6 more seats than the row in front.
This situation can be modeled by the following equation:
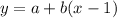
Where y is the number of seats in the current row, a is the number of seats in the first row, b is the number of additional seats in each new row, and x is the number of the row (we subtract 1 because we need to add 6 chairs, without taking into account the first row).
Let's check for the second row:
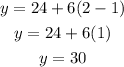
The second row has 6 more seats than the first row, now we have proved the equation works, we can apply it to the 6th row by replacing x=6:
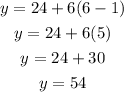
There are 54 seats in the 6th row.
The answer is C. 54