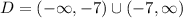Question

How For the pair of functions, find the indicated domain.

Answer 1

Step-by-step explanation

Finding the product of the given functions.

The product of two functions is defined as follows:

`(f\cdot g)(x)=(f)(x)\cdot(g)(x)`

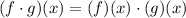
Then, we have:

`\begin{gathered} f(x)=(6)/(x+7) \\ g(x)=x+5 \\ (f\cdot g)(x)=(f)(x)*(g)(x) \\ (f\cdot g)(x)=(6)/(x+7)(x+5) \\ (f\cdot g)(x)=(6(x+5))/(x+7) \\ (f\cdot g)(x)=(6x+30)/(x+7) \end{gathered}`

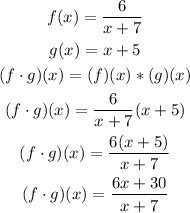
Finding the domain of f · g

Step 1: We set the denominator equal to 0 to find where the above expression is undefined.

`x+7=0`

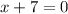
Step 2: We subtract 7 from both sides.

`\begin{gathered} x+7-7=0-7 \\ x=-7 \end{gathered}`

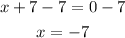
Step 3: Since the domain is all values of x that make the expression defined, the domain of f · g is all values of x different from -7.

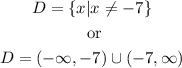
`\begin{gathered} D={}{}\lbrace x|x\\e-7\rbrace \\ \text{ or} \\ D=(-\infty,-7)\cup(-7,\infty) \end{gathered}`Answer
`D=(-\infty,-7)\cup(-7,\infty)`