The given triangle ABC and DEF are similar
From the properties of the similar triangle :
The ratio of the corresponding sides of similar traingle are equal and the ratio of perimeter is also equal to the ratio of corresponding sides
In the triangle ABC, AC=9, BC=6, and the angle B is 90 degree
then apply pythagoras to find the third side of triangle:
Pythagoras Theorem: The square of sum of base and perpendicular is equal to the square of Hypotenuse.
![\begin{gathered} \text{ By Pythagoras :} \\ AB^2=BC^2+CA^2 \\ AB^2=6^2+9^2 \\ AB^2=36+81 \\ AB^2=117 \\ AB=\sqrt[]{117} \\ AB=10.81 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/ht5ocfg7i7rozig3i3e3whbu594v7v4zfi.png)
Perimeter of Triangle is express as the sum of the length of all the sides of traingle
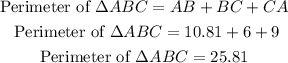
The scale Factor :
![\begin{gathered} \Delta ABC\text{ }\approx\Delta DEF \\ So, \\ (AB)/(DE)=(BC)/(EF)=(CA)/(FD) \\ \text{ Substitute the values and find the ratio} \\ (10.81)/(16.2)=(6)/(EF)=(9)/(FD) \\ 0.66=(6)/(EF)=(9)/(FD) \\ \text{ So, the scale factor = 0.66} \end{gathered}]()
Since the ratio of perimeter of triangle ABC and DEF are same as the ratio of thier corresponding sides
So,
![\begin{gathered} \frac{Perimeter\text{ of }\Delta ABC}{Perimeter\text{ of }\Delta DEF}=0.667 \\ \text{ Simplify for the perimeter of }\Delta DEF \\ Perimeter\text{ of }\Delta DEF=\frac{Perimeter\text{ of }\Delta ABC}{0.667} \\ \text{ Substitute the value of }Perimeter\text{ of }\Delta ABC=25.81 \\ Perimeter\text{ of }\Delta DEF=(25.81)/(0.667) \\ Perimeter\text{ of }\Delta DEF=38.69\text{ unit} \end{gathered}]()
So, Perimeter of triangle DEF = 38.69 unit