Question

I need help solving this last problem. It’s very challenging.

Answer 1

To solve this exercise you have to apply the rules of function transformation.

Considering y= f(x) as the parent function (before the transformation)

→ If you add a constant to the x-term of the function, the transformation will result in a horizontal translation to the left. So, y=f(x+k) indicates that the function was moved "k" units to the left.

→ If you subtract a constant to the x-term, the resulting movement will be a horizontal translation to the right. So y=f(x-k) indicates that the function was moved "k" units to the left.

→ If you add a constant to the function, the resulting movement will be a vertical translation up. So y=f(x)+c indicates that the function was moved "c" units up.

→ If you subtract a constant to the function, the resulting movement will be a vertical translation down. So, y=f(x)-x indicates that the function was moved "c" units down.

Given the transformation

`y=f(x+1)+1`

This indicates that the function was moved 1 unit to the left and 1 unit up.

If the parent function had vertex in the origin (0,0), subtract 1 unit from the x-coordinate and add 1 unit to the y-coordinate to determine the position of the vertex of the function after the translation:

`\begin{gathered} (x,y)\to(x-1,y+1) \\ (0,0)\to(0-1,0+1)=(-1,1) \end{gathered}`

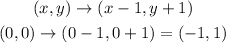
The vertex of the function after the translation will ve (-1,1), looking at the options, the only graph with the said vertex is graph A.