Question

Solve the system by elimination.5x - 6y + 3z = -2-2 + 4y = 102x - 2 = 2Pls see the picture

Answer 1

`\begin{gathered} 5x-6y+3z=-2 \\ -x+4y=10 \\ 2x-z=2 \end{gathered}`

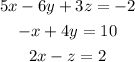
1) To solve the equation system by elimination, first, multiply the third equation by 3:

`\begin{gathered} 3(2x-z)=3\cdot2 \\ 3\cdot2x-3\cdot z=6 \\ 6x-3z=6 \end{gathered}`

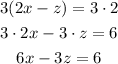
2) Add the result to the first equation:

`\begin{gathered} 5x+6x-6y+3z-3z=-2+6 \\ 11x-6y=4 \end{gathered}`

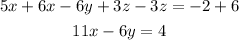
3) Next, multiply the second equation by 11

`\begin{gathered} 11(-x+4y)=11\cdot10 \\ 11\cdot(-x)+11\cdot4y=110 \\ -11x+44y=110 \end{gathered}`

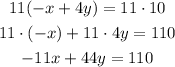
4) Add the expressions 11x-6y=4 and -11x+44y=110

`\begin{gathered} 11x-11x-6y+44y=4+110 \\ 38y=114 \end{gathered}`

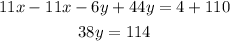
Divide both sides by 38 to determine the value of y:

`\begin{gathered} (38y)/(38)=(114)/(38) \\ y=3 \end{gathered}`

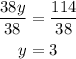
5) Replace the value of y in the second equation to determine the value of x:

`\begin{gathered} -x+4y=10 \\ -x+4\cdot3=10 \\ -x+12=10 \\ -x+12-12=10-12 \\ -x=-2 \\ (-1)(-x)=(-1)(-2) \\ x=2 \end{gathered}`

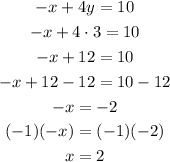
6) Replace the value of x in the third equation to determine the value of z:

`\begin{gathered} 2x-z=2 \\ 2\cdot2-z=2 \\ 4-z=2 \\ 4-4-z=2-4 \\ -z=-2 \\ z=2 \end{gathered}`

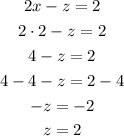
The solution of the equation system is x=2, y=3, and z=2